Leetcode 51. N-Queens

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

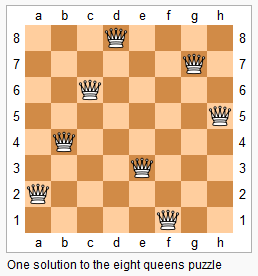
Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Thinking:

When the question asks about returning all the possible solutions. Backtracking is always the first method we should think about. Then we should think that whether it is a permutaion problem or combination problem. Typically, the combination needs to O(m x n)(two for loop) method to solve the problem and permutaion needs n!. And in this problem, it is a permutation problem. Then the problem is converted to a problem that how to write permutaion function.

Steps:

check whether input is valid;
Since we are going to use Permutation. We should decide how many parameters we need in permutation function. Typically, we will let result as an input parameter of the permutation function. Because permutation function is a void function. So we have to let result in the input parameter so that we can store the information. Also another method that can keep the information is to build a function with return value. But this need we to use Divide and Conquer to solve the problem, which is not suitable in the problem of permutaion.
Determine the return condition. We need to decide when the function when to return.

We should delete what we add at the end of the loop.(Backtracking).

Code:

class Pair{
 int x;
 int y;
 public Pair(int x, int y){
     this.x = x;
     this.y = y;
 }
}
public class Solution {
 public List<List<String>> solveNQueens(int n) {
     if(n <= 0) return new ArrayList<List<String>>();
     List<List<String>> result = new ArrayList<>();
     List<String> list = new ArrayList<>();
     List<Pair> set = new ArrayList<>();
     char[] output = new char[n];
     Arrays.fill(output,'.');
     permutationHelper(result, list,  set, 0, n, output);
     return result;
 }

 private void permutationHelper(List<List<String>> result, List<String> list, List<Pair> set, int level, int n, char[] output){
     if(list.size() == n){
         result.add(new ArrayList<String>(list));
         return;
     }

     for(int i = 0; i < n; i++){
         if(set.size() == 0){
             Pair Node = new Pair(level,i);
             set.add(Node);
             list.add(outputHelper(output,Node,n));
             permutationHelper(result, list,  set, level + 1, n,output);
             set.remove(set.size()-1);
             list.remove(list.size()-1);
         }
         else{
             int flag = 0;
             for(int j = 0; j < set.size(); j++){
                 Pair Node = set.get(j);
                 if(i == Node.y || Math.abs((double)(Node.y - i)/(double)(Node.x - level)) == 1.0){
                     flag = 1;
                     break;
                 }
             }
             if(flag == 0){
                 Pair Node = new Pair(level,i);
                 set.add(Node);
                 list.add(outputHelper(output,Node,n));
                 permutationHelper(result, list,  set, level + 1, n,output);
                 set.remove(set.size()-1);
                 list.remove(list.size()-1);
             }

         }
     }
 }

 private String outputHelper( char[] output, Pair Node , int n){
     char[] output2 = Arrays.copyOf(output,output.length);
     output2[Node.y] = 'Q';
     String str = new String(output2);
     return str;
 }
}

Conclusion:

We should be careful if we want to use slope to solve the problem. we should use double rather than int. Otherwise we can use x1 - x2 = y1 - y2/-(y1-y2), which can avoid this problem.

Leetcode 51. N-Queens